皆様こんにちはイマイです
Unity使っていると「面積求めたいなぁ」って思った時があったので実装方法を考えてみました。
できればUnityで用意されている関数を積極的に活用していきたいと考えています。
距離を求める関数Distance
Vector2.Distance – Unity スクリプトリファレンス
a と b の間の距離を返します
//a,bの距離を求める。(a,bはVector2) Vector2.Distance(a, b)
求める三角形の三点は以下のように定義します。
void Start () {
Vector2 A = new Vector2(1, 2);
Vector2 B = new Vector2(0, 10);
Vector2 C = new Vector2(10, 0);
Debug.Log(CalculateArea1(A, B, C));
}
それぞれの求め方のところに公式を書いておきます。
ヘロンの公式
辺の長さとヘロンの公式を使って面積を求めたものが以下になります。
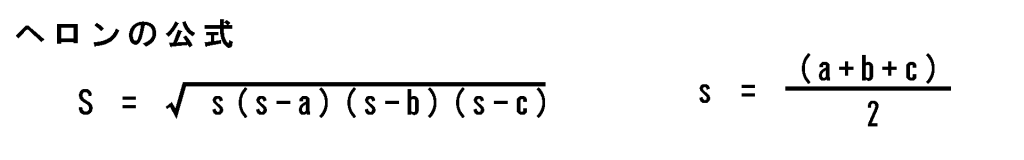
//ヘロンの公式を使って面積を求める
private float CalculateArea1(Vector2 A, Vector2 B, Vector2 C)
{
float S,s;
float a = Vector2.Distance(B, C);
float b = Vector2.Distance(A, C);
float c = Vector2.Distance(A, B);
s = (a+b+c)/2;
S = Mathf.Sqrt(s * (s - a) * (s - b) * (s - c));
return S;
}
底辺x高さx1/2で求める
3つの点のうち一つが原点にあると簡単にもとめることができます。
以下のサイトを参考に実装しました
座標平面上で三角形の面積を計算する公式 – 具体例で学ぶ数学
座標平面上で三角形の面積を計算する公式とその証明を解説します。1つの頂点が原点である場合は計算が簡単です。
//一点を原点に移動してそこから求める
private float CalculateArea2(Vector2 A, Vector2 B, Vector2 C)
{
float S;
Vector2 A2 = A;
Vector2 B2 = B;
Vector2 C2 =C;
//一点が原点に存在しないときの処理
if (A.magnitude != 0)
{
Vector2 A_delta = new Vector2(A.x,A.y);
A2 = new Vector2(A.x - A_delta.x, A.y - A_delta.y);
B2 = new Vector2(B.x - A_delta.x, B.y - A_delta.y);
C2 = new Vector2(C.x - A_delta.x, C.y - A_delta.y);
}
S = Mathf.Abs(B2.x * C2.y - C2.x * B2.y)*1/2;
return S;
}
2辺とその間の角が分かっている三角形
二辺の長さとその間の角をsinで求めるやつです。
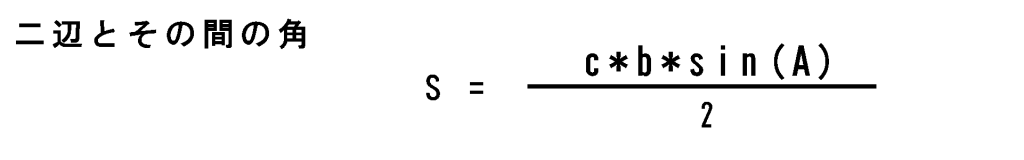
二点の角度を求めるのはAngle関数を使います。
Vector2.Angle – Unity スクリプトリファレンス
Returns the unsigned angle in degrees between from and to.
このAngleという関数は原点をもとに二点間の角度を求めるので
座標移動とラジアンに変換する必要があるので処理が冗長になってしまいますね。
//二辺の長さとその間の角度から求める
private float CalculateArea3(Vector2 A, Vector2 B, Vector2 C)
{
float S;
Vector2 A2 = A;
Vector2 B2 = B;
Vector2 C2 = C;
if (A.magnitude != 0)
{
Vector2 A_delta = new Vector2(A.x, A.y);
A2 = new Vector2(A.x - A_delta.x, A.y - A_delta.y);
B2 = new Vector2(B.x - A_delta.x, B.y - A_delta.y);
C2 = new Vector2(C.x - A_delta.x, C.y - A_delta.y);
}
float a = Vector2.Distance(B2, C2);
float b = Vector2.Distance(A2, C2);
float c = Vector2.Distance(A2, B2);
float angle = Vector2.Angle(B2, C2);
//angleは弧度法で返るのでラジアンに変換する
float rad = angle * (Mathf.PI / 180);
S = c * b * Mathf.Sin(rad) * 1/2;
return S;
}
外接円の半径から求める
外接円の半径をsinを使って求めた後三角形の面積を求めます。

//外接円の半径から求める
private float CalculateArea4(Vector2 A, Vector2 B, Vector2 C)
{
float S;
Vector2 A2 = A;
Vector2 B2 = B;
Vector2 C2 = C;
if (A.magnitude != 0)
{
Vector2 A_delta = new Vector2(A.x, A.y);
A2 = new Vector2(A.x - A_delta.x, A.y - A_delta.y);
B2 = new Vector2(B.x - A_delta.x, B.y - A_delta.y);
C2 = new Vector2(C.x - A_delta.x, C.y - A_delta.y);
}
float a = Vector2.Distance(B2, C2);
float b = Vector2.Distance(A2, C2);
float c = Vector2.Distance(A2, B2);
float angle = Vector2.Angle(B2, C2);
//angleは弧度法が返るのでラジアンに変換する
float rad = angle * (Mathf.PI / 180);
//外接円の半径
float R = a / (2*Mathf.Sin(rad));
S = (a * b * c)/(4 * R);
return S;
}
書いてみると一番上のヘロンの公式が一番すっきりしていますね。
他にも公式あるかもしれないです~
もし間違っているところありましたらご指摘いただけると幸いです。
今回は2Dでしたが次の記事で3Dの時の方も書きます!
あと多角形の時も書く予定です~
それではよいハッキングライフを~